Curriculum
Groupe de permutations
Définition et exemples
0/1Éléments remarquables de Sn
0/1Groupes alternés
0/1Éléments remarquables de Sn
Définition:
Soient ![]() tels que
tels que ![]() . On appelle transposition associé à
. On appelle transposition associé à ![]() et
et ![]() la permutation notée
la permutation notée ![]() ou
ou ![]() de
de ![]() définie par
définie par
![Rendered by QuickLaTeX.com \[\begin{array}{rccl}T_{ij}:&\{1;2;\cdots;n\}&\rightarrow& \{1;2;\cdots;n\}\\&x&\mapsto& T_{ij}(x)=\left\{\begin{array}{ll}j, & \hbox{\text{ si } }x=i; \\i, & \hbox{\text{ si } } x=j;\\x, & \hbox{\text{ sinon. } }\end{array}\right.\end{array}\]](https://www.lucdiekouam.cm/wp-content/ql-cache/quicklatex.com-a3c0f9cea188e5f2c20ce74cece9c7f8_l3.png)
Remarque: ![]() . Le nombre de transposition de
. Le nombre de transposition de ![]() est
est ![]()
Propriété:
- [
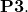 ]
] 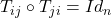
- [
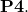 ]
] 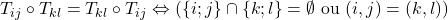
Preuve:
Soit ![]()
- si
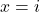 alors
alors 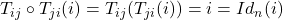
- si
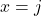 alors
alors 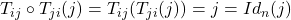
- si
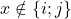 alors
alors 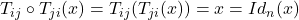

Théorème:
l’ensemble des transpositions est une partie génératrice de ![]() .
.
Preuve:
pour ![]() ,
, ![]() ;
; ![]()
Pour ![]()
![]()
Par conjecture on obtient le résultat qui nécessite une preuve plus rigoureuse.![]()
Définition:
soit ![]() On appelle orbite d’un élément
On appelle orbite d’un élément ![]() pour
pour ![]() l’ensemble
l’ensemble ![]() .
.
Il est noté ![]() ; mais pour faire simple on notera
; mais pour faire simple on notera ![]() .
.
Exemple: Dans ![]() déterminer toutes les orbites de
déterminer toutes les orbites de ![]()
Proposition:
Soit ![]() , la relation
, la relation ![]() définie sur
définie sur ![]() par
par
![]()
est une relation d’équivalence sur ![]() .
.
Preuve: TD ![]()
Définition:
Soit ![]() on appelle
on appelle ![]() -cycle de
-cycle de ![]() toute permutation
toute permutation ![]() dont toutes les orbites sont des singletons sauf une qui est de cardinal
dont toutes les orbites sont des singletons sauf une qui est de cardinal ![]()
Exemple:
Les transpositions sont des ![]() -cycles
-cycles
La permutation ![]() est un
est un ![]() -cycle.
-cycle.
Dans ![]()
![]() est un
est un ![]() -cycle.
-cycle.
Définition:
On appelle support d’une permutation l’ensemble des éléments non invariants.
![]()
Propriété:
- [
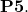 ] L’ordre d’un
] L’ordre d’un  -cycle
-cycle 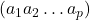 est exactement sa longueur ‘
est exactement sa longueur ‘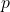 ‘.
‘. - [
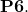 ] Si
] Si  est un
est un 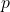 -cycle alors
-cycle alors 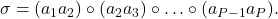 C’est à dire que
C’est à dire que 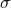 se décompose en produit de
se décompose en produit de 
transpositions.
Théorème:
Toute permutation différente de ![]() se décompose de manière unique à l’ordre près en produit de cycles disjoints.
se décompose de manière unique à l’ordre près en produit de cycles disjoints.
Preuve: TD(Bien utiliser les orbites)![]()
Exemple: On donne
![]()
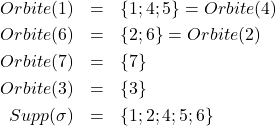
Décomposition de ![]() en produit de cycles.
en produit de cycles.
![]() ou
ou ![]()
En produit de transpositions on a: ![]()
Déterminer l’ordre de ![]()
Remarque: L’ordre d’une permutation quelconque de ![]() est le ppcm des ordres des cycles disjoints qui apparaissent dans sa décomposition(ces cycles sont des longueurs
est le ppcm des ordres des cycles disjoints qui apparaissent dans sa décomposition(ces cycles sont des longueurs ![]() )
)